Variational Quantum Eigensolver (VQE)#
The tutorial requires qiskit-nature package which can be installed with these instructions. The tutorial assumes that the user is familiar with VQE. User’s can follow the Ground State Solvers tutorial by qiskit-nature for the same.
[1]:
"""Variational Quantum Eigensolver (VQE) tutorial."""
from IPython.display import clear_output
import matplotlib.pyplot as plt
import numpy as np
from qiskit_nature.units import DistanceUnit
from qiskit_nature.second_q.drivers import PySCFDriver
from qiskit_nature.second_q.mappers import JordanWignerMapper
from qiskit_nature.second_q.circuit.library import HartreeFock
from qiskit_nature.second_q.algorithms import GroundStateEigensolver
from qiskit_nature import settings
from qiskit_algorithms.utils import algorithm_globals
from qiskit.circuit.library import EfficientSU2
from qiskit_algorithms.optimizers import L_BFGS_B
from qiskit_algorithms.minimum_eigensolvers import NumPyMinimumEigensolver, VQE
from qiskit_qulacs.qulacs_estimator import QulacsEstimator
from qiskit_qulacs.qulacs_estimator_gradient import QulacsEstimatorGradient
settings.use_pauli_sum_op = False
algorithm_globals.random_seed = 42
[2]:
driver = PySCFDriver(
atom="H 0 0 0; H 0 0 0.735",
basis="sto3g",
charge=0,
spin=0,
unit=DistanceUnit.ANGSTROM,
)
[3]:
problem = driver.run()
fermionic_op = problem.hamiltonian.second_q_op()
mapper = JordanWignerMapper()
qubit_op = mapper.map(fermionic_op)
print(qubit_op)
SparsePauliOp(['IIII', 'IIIZ', 'IIZI', 'IIZZ', 'IZII', 'IZIZ', 'ZIII', 'ZIIZ', 'YYYY', 'XXYY', 'YYXX', 'XXXX', 'IZZI', 'ZIZI', 'ZZII'],
coeffs=[-0.81054798+0.j, 0.17218393+0.j, -0.22575349+0.j, 0.12091263+0.j,
0.17218393+0.j, 0.16892754+0.j, -0.22575349+0.j, 0.16614543+0.j,
0.0452328 +0.j, 0.0452328 +0.j, 0.0452328 +0.j, 0.0452328 +0.j,
0.16614543+0.j, 0.17464343+0.j, 0.12091263+0.j])
[4]:
print("Number of qubits:", qubit_op.num_qubits)
print("Number of hamiltonian terms:", len(qubit_op))
Number of qubits: 4
Number of hamiltonian terms: 15
[5]:
# Get reference solution
numpy_solver = NumPyMinimumEigensolver()
calc = GroundStateEigensolver(mapper, numpy_solver)
res_actual = calc.solve(problem)
print(res_actual)
=== GROUND STATE ENERGY ===
* Electronic ground state energy (Hartree): -1.857275030202
- computed part: -1.857275030202
~ Nuclear repulsion energy (Hartree): 0.719968994449
> Total ground state energy (Hartree): -1.137306035753
=== MEASURED OBSERVABLES ===
0: # Particles: 2.000 S: 0.000 S^2: 0.000 M: 0.000
=== DIPOLE MOMENTS ===
~ Nuclear dipole moment (a.u.): [0.0 0.0 1.3889487]
0:
* Electronic dipole moment (a.u.): [0.0 0.0 1.388948701555]
- computed part: [0.0 0.0 1.388948701555]
> Dipole moment (a.u.): [0.0 0.0 -0.000000001555] Total: 0.000000001555
(debye): [0.0 0.0 -0.000000003953] Total: 0.000000003953
[6]:
exact_energy = res_actual.eigenvalues[0]
print(f"Expected ground state energy: {exact_energy:.12f} Ha")
Expected ground state energy: -1.857275030202 Ha
[7]:
# Hartree focks state
num_particles = problem.num_particles
num_spatial_orbitals = problem.num_spatial_orbitals
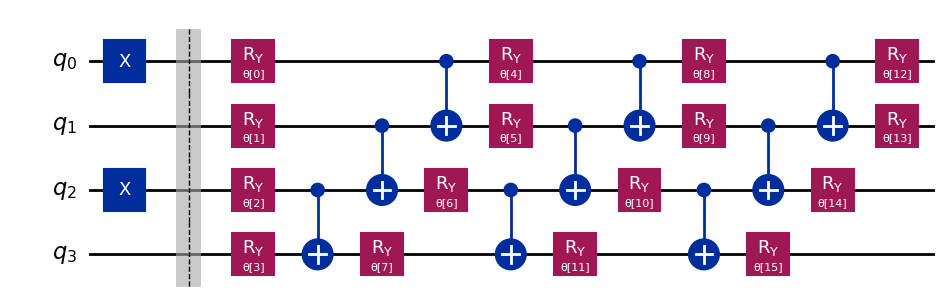
init_state = HartreeFock(
num_spatial_orbitals=num_spatial_orbitals,
num_particles=num_particles,
qubit_mapper=mapper,
)
# ansatz
ansatz = EfficientSU2(qubit_op.num_qubits, su2_gates=["ry"]).decompose()
# Add the initial state
init_state.barrier()
ansatz = init_state.compose(ansatz)
ansatz.draw("mpl")
[7]:
[8]:
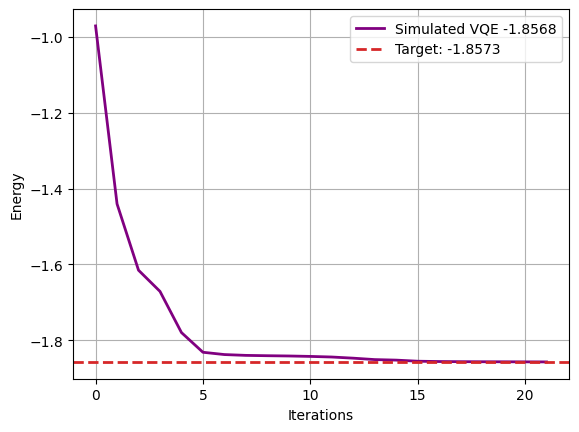
intermediate_info = []
def callback(eval_count, parameters, value, std): # pylint: disable=unused-argument
"""
A callback that can be registered with the optimizer to store the intermediate
value and parameters.
"""
intermediate_info.append(value)
clear_output(wait=True)
plt.plot(
intermediate_info,
color="purple",
lw=2,
label=f"Simulated VQE {np.round(value,4)}",
)
plt.ylabel("Energy")
plt.xlabel("Iterations")
# Exact ground state energy value
plt.axhline(
y=exact_energy,
color="tab:red",
ls="--",
lw=2,
label="Target: " + str(np.round(exact_energy, 4)),
)
plt.legend()
plt.grid()
plt.show()
[9]:
optimizer = L_BFGS_B(maxiter=20)
We use primitives from qiskit-qulacs of computing the expectation value and gradient.
[10]:
qulacs_estimator = QulacsEstimator()
qulacs_gradient = QulacsEstimatorGradient()
vqe = VQE(
qulacs_estimator, ansatz, optimizer, callback=callback, gradient=qulacs_gradient
)
result = vqe.compute_minimum_eigenvalue(operator=qubit_op)
[11]:
print(result)
{ 'aux_operators_evaluated': None,
'cost_function_evals': 22,
'eigenvalue': -1.8567922267701444,
'optimal_circuit': <qiskit_nature.second_q.circuit.library.initial_states.hartree_fock.HartreeFock object at 0x7dcf14be65c0>,
'optimal_parameters': { ParameterVectorElement(θ[0]): 3.596756540143855,
ParameterVectorElement(θ[1]): -1.3110309933022815,
ParameterVectorElement(θ[2]): 5.32593579823301,
ParameterVectorElement(θ[3]): 1.209594897445057,
ParameterVectorElement(θ[4]): -5.154494260584071,
ParameterVectorElement(θ[5]): 5.666947151363986,
ParameterVectorElement(θ[6]): 2.574344487887185,
ParameterVectorElement(θ[7]): 2.442111235436972,
ParameterVectorElement(θ[8]): -5.410130960542183,
ParameterVectorElement(θ[9]): -1.261167613799997,
ParameterVectorElement(θ[10]): -0.9072274382239279,
ParameterVectorElement(θ[11]): 4.979937294664101,
ParameterVectorElement(θ[12]): 2.755549835643336,
ParameterVectorElement(θ[13]): 3.4937762155898726,
ParameterVectorElement(θ[14]): 0.138866002148125,
ParameterVectorElement(θ[15]): -3.654455036700532},
'optimal_point': array([ 3.59675654, -1.31103099, 5.3259358 , 1.2095949 , -5.15449426,
5.66694715, 2.57434449, 2.44211124, -5.41013096, -1.26116761,
-0.90722744, 4.97993729, 2.75554984, 3.49377622, 0.138866 ,
-3.65445504]),
'optimal_value': -1.8567922267701444,
'optimizer_evals': None,
'optimizer_result': <qiskit_algorithms.optimizers.optimizer.OptimizerResult object at 0x7dcf14c184f0>,
'optimizer_time': 3.0805983543395996}
[12]:
def rel_err(target, measured):
"""Compute the relative error."""
return abs((target - measured) / target)
[13]:
# Compute the relative error between the expected ground state energy and the VQE's output
rel_error = rel_err(exact_energy, result.eigenvalue)
print(f"Expected ground state energy: {exact_energy:.12f}")
print(f"Computed ground state energy: {result.eigenvalue:.12f}")
print(f"Relative error: {rel_error:.12f}")
Expected ground state energy: -1.857275030202
Computed ground state energy: -1.856792226770
Relative error: 0.000259952578